The buffer capacity definition and formula derivation
Buffer solution is able to retain almost constant pH when small amount of acid/base is added. Quantitative measure of this resistance to pH changes is called buffer capacity.
Buffer capacity can be defined in many ways. You may find it defined as "maximum amount of either strong acid or strong base that can be added before a significant change in the pH will occur". This definition - instead of explaining anything - raises a question "what is a significant change?" - sometimes even change of 1 unit doesn't matter too much, sometimes - especially in biological systems - 0.1 unit change is a lot. Buffer capacity can be also defined as quantity of strong acid or base that must be added to change the pH of one liter of solution by one pH unit. Such definition - although have its practical applications - gives different values of buffer capacity for acid addition and for base addition (unless buffer is equimolar and its pH=pKa). This contradicts intuition - for a given buffer solution its resistance should be identical regardless of whether acid or base is added.
Buffer capacity definition that takes this intuition into account is given by
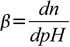 19.1
19.1where n is number of equivalents of added strong base (per 1 L of the solution). Note that addition of dn moles of acid will change pH by exactly the same value but in opposite direction. We will derive formula connecting buffer capacity with pH, pKa and buffer concentration. Derivation shown is based on Adam Hulanicki book Reakcje kwasów i zasad w chemii analitycznej, 2nd ed., PWN, Warszawa 1980 (English edition: Reactions of acids and bases in analytical chemistry; Chichester, West Sussex, England: E. Horwood; New York: Halsted Press, 1987).
To make further calculations easier let's assume that the strong base added is monoprotic, we also assume volume of 1 which will allow us to treat concentration and number of moles interchangeably. Charge balance of the solution is given by the equation (identical to 11.6):
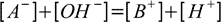 19.2
19.2[B+] is nothing else but concentration of the strong base present (or - as a volume is 1 - number of moles of strong base present) in the solution - thus it is n from 19.1 definition.
Total concentration of the buffer, Cbuf, is given by
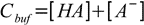 19.3
19.3From dissociation constant definition we have
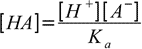 19.4
19.4so
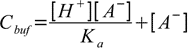 19.5
19.5or
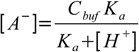 19.6
19.6Equations 19.2, 19.6 and water ionization constant definition when combined give us formula for the amount of the strong base:
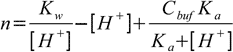 19.7
19.7Now we are ready to calculate derivative:
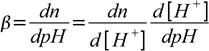 19.8
19.8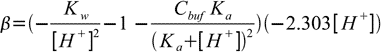 19.9
19.9So finally buffer capacity is given by
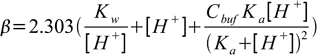 19.10
19.10This equation can be easily generalized for buffer capacity of solutions containing several buffers:
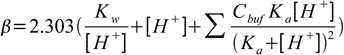 19.11
19.11Note that first two terms in the buffer capacity formula are not dependent on the buffer presence in the solution. They reflect the fact that solutions of high (or low) pH are resistant to pH changes. As it was already signalled in the buffer pH section, such solutions have high buffer capacity regardless of the presence (or lack of the presence) of a classic buffer. For table of example values of buffer capacities see buffer capacity discussion at buffer lectures.
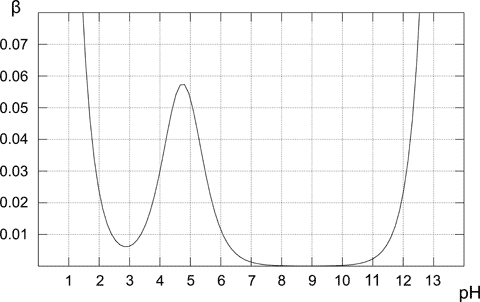
Above plot shows how the buffer capacity changes for the 0.1M solution of acetic buffer. As expected buffer exhibits the highest resistance to acid and base addition for the equimolar solution (when pH=pKa). From the plot it is also obvious that buffer capacity has reasonably high values only for pH close to pKa value. The further from the optimal value, the lower buffer capacity of the solution. Solution containing only conjugate base (pH 8-10) has buffer capacity of zero, for the higher pH presence of the strong base starts to play an important role. In the case of pure acetic acid solution (pH below 3) pH is already low enough to be resistant to changes due to the high concentration of H+ cations.
Note, that our buffer calculator (Buffer Maker) uses buffer capacities to select best buffer from its database for a given pH. It also calculates buffer capacity plots, to help you in buffer selection.



