Calculation of pH of a weak acid/base solution
pH of solution of any acid is described by the universal equation 6.9. Let's see what we can do to simplify the problem in case of weak acid.
We have to start with the general set of equations:
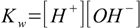 8.1
8.1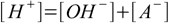 8.2
8.2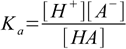 8.3
8.3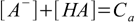 8.4
8.4If the acid is not very diluted and not extremely weak (in other words if ions from water dissociation can be neglected) equation 8.2 takes form
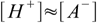 8.5
8.5which reflects stoichiometry of dissociation. At this moment we can also remove water ion product from our set, as [OH-] is no longer present in any other equation. Thus we are left with the equations 8.3, 8.4 and 8.5. Substituting [H+] for [A-] in 8.3 gives
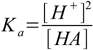 8.6
8.6From 8.4
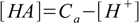 8.7
8.7which we will insert into 8.6 to get
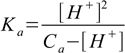 8.8
8.8or in polynomial form
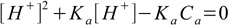 8.9
8.9This is quadratic equation for [H+] concentration with two roots, of which only one is positive:
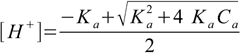 8.10
8.10It is worth of noting here, that the equation 8.8 is identical with the result obtained when using so called ICE (Initial, Change, Equilibrium) method for weak acid dissociation.
Note, that for a very weak acids - when Ka approaches 0 - numerator also approaches zero and result of pH calculation can be higher than 7. For example using pKa=14 and Ca=0.01 M we get pH=8. That's the effect of neglecting water dissociation, similar to the one observed when we used equation 7.6 for strong acids.
Using 5% rule we can make one more assumption to further simplify the calculation of pH. If [H+] is less than 5% of Ca we can put
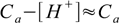 8.11
8.11and equation 8.6 takes form
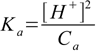 8.12
8.12or just
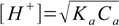 8.13
8.13Interestingly the same result can be obtained using two other methods. If you assume that the dissociation fraction is less than 5% - the equation 8.4 can be simplified to
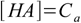 8.14
8.14which - when combined with 8.3 and 8.5 and solved - gives exactly 8.13. Also equation 8.10 can be simplified. First, KaCa product is in most cases much larger than Ka2 so 8.10 takes form
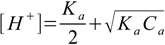 8.15
8.15Also in most cases
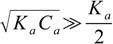 8.16
8.16so neglecting Ka/2 we get equation 8.13 once again
What is validity of these equations? Let's compare results of pH calculation of acetic (ethanoic) acid solution, with pKa=4.75, done using all three calculation methods. Numbers in parentheses are dissociation fractions calculated for the pH shown.
| Ca (M) | pH calculator | pH eq. 8.10 | pH eq. 8.13 |
|---|---|---|---|
| 1 | 2.38 (0.004) | 2.38 (0.004) | 2.37 (0.004) |
| 0.1 | 2.88 (0.013) | 2.88 (0.013) | 2.87 (0.013) |
| 0.01 | 3.38 (0.041) | 3.38 (0.041) | 3.37 (0.042) |
| 10-3 | 3.90 (0.125) | 3.90 (0.125) | 3.87 (0.133) |
| 10-4 | 4.47 (0.342) | 4.47 (0.342) | 4.37 (0.422) |
| 10-5 | 5.15 (0.714) | 5.15 (0.714) | 4.87 (1.334) |
| 10-6 | 6.02 (0.949) | 6.02 (0.949) | 5.37 (4.217) |
| 5×10-7 | 6.30 (0.972) | 6.31 (0.980) | 5.53 (5.96) |
| 10-7 | 6.79 (0.991) | 7.00 (0.994) | 5.87 (13.335) |
| 10-8 | 6.98 (0.994) | 8.00 (0.999) | 6.37 (42.170) |
As you see up to dissociation fraction of about 5% (0.05) all equations give exact result - so you should use the simplest one 8.13. Once the dissociation fraction gets higher than 5% equation 8.13 starts to give wrong results (with ridiculous dissociation fraction higher than 100%). Equation 8.10 holds much longer as it is unaffected by the changes in dissociation fraction. Its reign ends when the solution is so diluted that water dissociation can't be neglected no longer. It is time for the full equation 6.9.
We will check also results of pH calculation for other, much weaker acid - hydrocyanic (HCN) with pKa=9.31.
| Ca (M) | pH calculator | pH eq. 8.10 | pH eq. 8.13 |
|---|---|---|---|
| 1 | 4.66 (0.000) | 4.66 (0.000) | 4.65 (0.000) |
| 0.1 | 5.15 (0.000) | 5.16 (0.000) | 5.15 (0.000) |
| 0.01 | 5.65 (0.000) | 5.66 (0.000) | 5.65 (0.000) |
| 10-3 | 6.15 (0.001) | 6.16 (0.001) | 6.15 (0.001) |
| 10-4 | 6.62 (0.002) | 6.66 (0.002) | 6.65 (0.002) |
| 10-5 | 6.91 (0.004) | 7.16 (0.007) | 7.15 (0.007) |
| 10-6 | 6.99 (0.005) | 7.66 (0.022) | 7.65 (0.022) |
| 5×10-7 | 6.99 (0.005) | 7.81 (0.031) | 7.80 (0.031) |
| 10-7 | 7.00 (0.005) | 8.17 (0.068) | 8.15 (0.070) |
| 10-8 | 7.00 (0.005) | 8.70 (0.198) | 8.65 (0.221) |
As dissociation fraction is always very low results from both simplified equations are almost identical - but they are wrong once the concentration of acid falls below 10-4 M when the water dissociation enters the scene. Conclusion is - the weaker the acid, the earlier results from simplified equations are wrong.
Information on both equations usability can be also presented on the plot. Axes are selected in such a way, that the further we move from the (0,0) point the weaker and/or more diluted acid is:
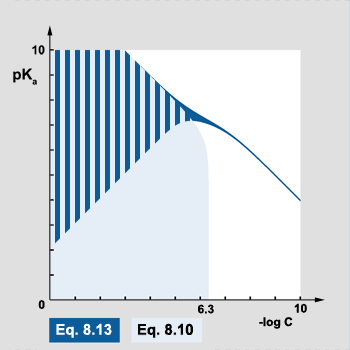 pic. 8.1
pic. 8.1
Area marked in dark blue is where the most simplified equation 8.13 can be used, light blue - where equation 8.10 gives correct results. In the striped area both equations give correct results. Correct results means here that the difference between exact and approximate pH value is less than 0.02 pH unit. White area to the right is where only full cubic equation 6.9 gives correct results. Large part of this area are solutions that are simply neutral.
Dark blue "tail" in the right part of the plot is an interesting area where equation 8.13 gives correct results by chance. In this area all solutions are neutral (acid concentration is below 5×10-7) and for every pKa value one can easily find acid concentration that - when entered into 8.13 - gives 10-7 as H+ concentration. This correct result is a sheer coindicidence.
In case of weak bases you use exactly the same assumptions for calculations, the only difference is that it is much more convenient to calculate [OH-] and pOH and to convert it into pH, than to do the calculations for [H+] from the start. But it is possible - and for example weak base version of equation 8.13
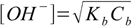 8.17
8.17can be converted to
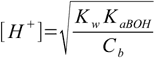 8.18
8.18See also weak acid question 1 and weak acid question 2 in our questions section.
You may check also our pH cheat sheet.



