Calculation of pH of polyprotic acid/base solution
Calculations of pH of polyprotic acids and bases are much more difficult and in many cases there are no simplifying assumptions that can be used. Thus often we are forced to use the most general approach.
Let's see how this can be done for H2A acid - similar derivation can be done in case of acids (and bases) that have more dissociation steps.
We will use overall dissociation constants for calculations (they can be easily calculated from stepwise ones, as described in the polyprotic acid constants section):
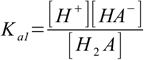 9.1
9.1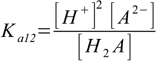 9.2
9.2Our other equations are - as usual - water ion product
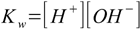 9.3
9.3and two balances - mass:
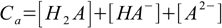 9.4
9.4and charge:
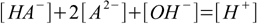 9.5
9.5which we can rewrite instantly in the form
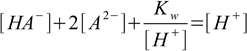 9.6
9.6removing [OH-] and equation 9.3 from further calculations.
Our task is to combine above into one equation containing only constants and [H+]. To do so we will first solve 9.1 and 9.2 for A2- and HA- respectively:
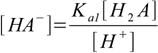 9.7
9.7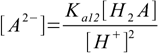 9.8
9.8Putting these into mass balance equation 9.4 gives
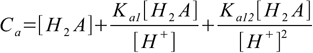 9.9
9.9or
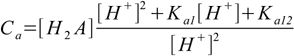 9.10
9.10This can be solved for [H2A]:
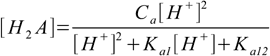 9.11
9.11Substituting 9.11 into 9.7 and 9.8 yields
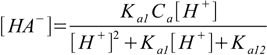 9.12
9.12and
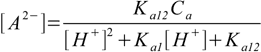 9.13
9.13We are almost ready. In both 9.12 and 9.13 the only unknown concentration present on the right side of the equation is [H+]. All we have to do now is to substitute 9.12 and 9.13 into 9.6. After some rearranging we will get
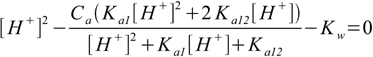 9.14
9.149.14 is not in polynomial form that is best for numerical calculations, however, it is not very difficult to convert into polynomial form, besides, form shown is pretty compact and easy to expand to acids with more protons. It is also worth of noting that if you assume Ka12=0 equation 9.14 simplifies to 6.8.
For the polyprotic weak base solution the same approach yields very similar equation.
Equation 9.14 will give good results always (if you dare to solve it by yourself instead of using pH calculator), however, there are cases when we can try to calculate pH looking for simplifications.



