Simplified methods of pH calculation of amphiprotic salt solution
As usual, the most general approach is unsuitable for calculations done by hand. For salts with one strong and one weak component the best way of pH calculation it to treat conjugate acid (or base) as the only source of H+ (or OH-) ions, and do the calculations in the same way as it was described in weak/acid base section.
For example if we have a solution of a salt of a weak acid (with dissociation constant Ka) and a strong base, the reaction of hydrolysis is
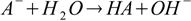
and the equilibrium is described by the conjugate base dissociation constant
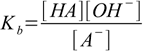 13.1
13.1where
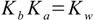 13.2
13.2Starting from these equations we can calculate pOH and pH of the solution using method and assumptions shown for weak acid an base. Exactly the same approach can be used for salt of strong acid and weak base - just using the Ka constant for the weak base conjugate acid . If the acid (or base) is polyprotic we can use one of the methods described in the polyprotic simplified section.
However, what to do when we have a solution of a salt that contains both weak acid and weak base? In general we should use the full equation derived on the pH of the salt solution page. As it yields 4th degree polynomial, its applicability is at least questionable. Luckily, if the solution is not too diluted we can easily derive much simpler formula.
Let's say we have a solution of an AB salt of a weak acid and a weak base of concentration C and dissociation constants Ka and Kb. Equations for Ka and Kb have their standard forms:
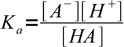 13.3
13.3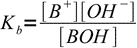 13.4
13.4We will solve them for [H+] and [OH-]:
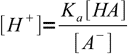 13.5
13.5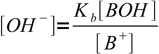 13.6
13.6Putting calculated concentrations into water ion product equation we get:
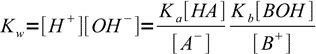 13.7
13.7or
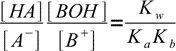 13.8
13.8Now let's take a look at the charge balance equation:
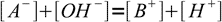 13.9
13.9As long as we deal with not very diluted solution, we can safely assume concentrations of both H+ and OH- are much lower than concentrations of A- and B+. That yields an important approximation:
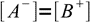 13.10
13.10From the mass balance we know that
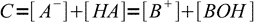 13.11
13.11combining it with the equation 13.10 we get another approximation:
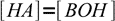 13.12
13.12Using 13.10 and 13.12 we can now rewrite equation 13.8 as
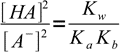 13.13
13.13which is a very important result. Knowing ratio of concentrations of the acid and its conjugate base we can easily calculate H+ concentration, just by rearranging acid dissociation formula and plugging the ratio into:
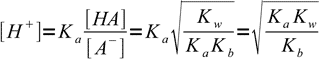 13.14
13.14Taking logs of both sides:
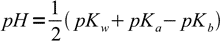 13.15
13.15If we remember the relation between Ka and Kb we can rewrite this equation as
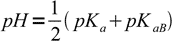 13.16
13.16where pKaB is acid dissociation constant of the base B conjugate acid. This result is interesting, as the equation is identical to that derived for the pH of solution of the amphiprotic salt.
How good is the equation 13.16? For ammonium acetate (CH3COONH4) pKa=4.75 and pKb=4.75 too. This salt is so symmetrical, that results of pH calculation just must be perfect:
| C (M) | pH calculator | pH eq. 13.16 |
|---|---|---|
| 1 | 7.00 | 7.00 |
| 10-8 | 7.00 | 7.00 |
And what about aniline formate? pKa=3.745 and pKb=9.4, so there is a substantial difference in the strengths.
| C (M) | pH calculator | pH eq. 13.16 |
|---|---|---|
| 1 | 4.17 | 4.17 |
| 0.1 | 4.17 | 4.17 |
| 0.01 | 4.18 | 4.17 |
| 0.001 | 4.24 | 4.17 |
The more diluted the solution, the worse the results, but if the solution is at least in 0.01M range both equations - 12.9 and 13.16 - give acceptable results.



