Calculation of pH of a strong acid/base solution
If the acid is strong we can assume it is fully dissociated. If so, there are no HA molecules in the solution and instead of dissociation equilibrium we can write
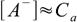 7.1
7.1Still, there are two sources of H+ cations - acid and water autoionization. This is reflected by the charge balance and water ion product:
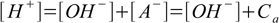 7.2
7.2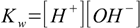 7.3
7.3When solved this gives
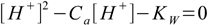 7.4
7.4This equation is much easier to use than the full equation 6.9 derived in acid-base solution section and it describes any solution of acid strong enough to be fully dissociated, regardless of its concentration. However, there is one more assumption to make, that will make our calculations even easier. Let's take a look at charge balance equation in the 7.2 form:
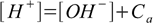 7.5
7.5If the concentration Ca is large enough [OH-] value is so small, that it can be omitted from the sum on the right side of the equation, giving:
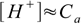 7.6
7.6which is the simplest form possible (and not far from 7.1). But how accurate are these simplified formulas?
Let's take a look at results for pH calculation of hydrochloric acid solutions (pKa=-4). pH calculator results were found using BATE (general approach without simplifications):
| Ca (M) | pH calculator | pH eq. 7.6 | pH eq. 7.4 |
|---|---|---|---|
| 1 | 0.00 | 0.00 | 0.00 |
| 0.1 | 1.00 | 1.00 | 1.00 |
| 0.01 | 2.00 | 2.00 | 2.00 |
| 10-3 | 3.00 | 3.00 | 3.00 |
| 10-4 | 4.00 | 4.00 | 4.00 |
| 10-5 | 5.00 | 5.00 | 5.00 |
| 10-6 | 6.00 | 6.00 | 6.00 |
| 5×10-7 | 6.28 | 6.30 | 6.28 |
| 10-7 | 6.79 | 7.00 | 6.79 |
| 10-8 | 6.98 | 8.00 | 6.98 |
Equation 7.6 is accurate up to (or rather down to) concentration of 5×10-7 M. Below effect of water autoionization starts to play important role.
And what about the assumption that strong acids are fully dissociated? If it is not true, the effect will be visible for high concentrations. Nitric acid - although strong - has pKa=-1 and is much weaker than the hydrochloric acid.
| Ca (M) | pH calculator | pH eq. 7.6 | pH eq. 7.4 |
|---|---|---|---|
| 1 | 0.04 | 0.00 | 0.00 |
| 0.5 | 0.32 | 0.30 | 0.30 |
| 0.1 | 1.00 | 1.00 | 1.00 |
| 0.01 | 2.00 | 2.00 | 2.00 |
As expected - for high concentrations pH values calculated using simplified equation are a little bit lower than the ones calculated using without any assumptions. When we will move to the weak acids this effect will be crucial. It is worth of noting here that in case of strong acids our results will be additionally modified by the activity coefficients as the solutions in which we are looking for undissociated molecules are concentrated and they have high ionic strength.
In case of strong bases situation is identical, and the equations 7.4 and 7.6 take forms:
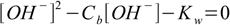 7.7
7.7and
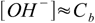 7.8
7.8However, there is one small difference - even the strongest bases are relatively weak. pKb for KOH is 0.5, so we may expect larger differences in results of pH calculations for concentrated solutions:
| Cb (M) | pH calculator | pH eq. 7.8 | pH eq. 7.7 |
|---|---|---|---|
| 1 | 13.63 | 14.00 | 14.00 |
| 0.5 | 13.43 | 13.70 | 13.70 |
| 0.1 | 12.90 | 13.00 | 13.00 |
| 0.01 | 11.99 | 12.00 | 12.00 |
| 10-7 | 7.21 | 7.00 | 7.21 |
| 10-8 | 7.02 | 6.00 | 7.02 |
For diluted solutions results are identical to these for strong acids (in both cases pH of 10-8 solution differs from neutral by 0.02 pH unit). However, for concentrated solutions differences are much higher and both simplified equations give wrong results.
You may also check our pH cheat sheet.



