The ionic strength and activity coefficients definitions
As it was already signaled in the introduction, all equilibrium calculations done using concentrations are wrong. Ions are charged so they interact in the solution attracting and repelling each other with coulomb forces. These interactions influence ions behavior and don't allow to treat every ion in the solution independently. Whole phenomenon - although investigated for over 100 years - is still not fully understood and described. To be precise in our equilibrium calculations instead of using concentrations we should use ions activities. Activities are not a theoretical construct - they can be measured for every solution. In fact whenever you put pH electrode into a solution you are measuring not [H+] but activity of H+ ions. It is enough to add an inert salt to the solution of a known acid to observe pH change that confirms activity concept (and is in accordance with the results of calculations presented below).
Most popular method used to calculate ions activities is the one proposed by Debye and Hückel in 1923.
First step in calculations is calculation of so called ionic strength, using the following formula:
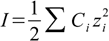 17.1
17.1where Ci is a molar concentration of ith ion present in the solution and zi is its charge. Summation is done for all charged molecules present in the solution.
Second step is calculation of activity coefficients given by the formula:
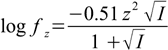 17.2
17.2An activity coefficient for all ions bearing the same charge is identical (although there exists slightly more precise formula in which activity coefficient is also a function of the ion radius).
And now the most important thing. The activity of any ion (with a charge z) is
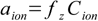 17.3
17.3where fz denotes the activity coefficient for z-charged ions.
Equilibrium calculations made using this approach give good results for ionic strength lower than 0.1. There are other theories, that work for higher ionic strengths, but they are based on experimentally determined coefficients that depend on types of ions present in the solution. There are no extensive tables of these coefficients, so their use is rather limited.
In all reaction quotients used throughout all sections we should replace concentrations of all ions with their activities. Mass and charge balances should use analytical concentrations of ions.
What error are we making neglecting ionic strength of the solution? Let's see what will happen if we prepare 0.05M phosphoric buffer pH 7.2 neglecting - and not neglecting - ionic strength of the solution. You can calculate pH of such a buffer using pH calculator - select phosphoric acid and sodium hydroxide from the databases and enter 0.05M as concentration of phosphoric acid and 0.075M as concentration of NaOH. This results in equimolar solution of sodium hydrogen phosphate and sodium dihydrogen phosphate. As pKa2 of the phosphoric acid is 7.20 we may expect this solution to have pH=7.20 (see Henderson-Hasselbalch equation - when both concentrations are identical, pH of the solution simply equals pKa). However, ionic strength of the solution is 0.1 (limit of the Debye-Hückel theory applicability), thus we can't neglect activity coeffcients - to take into account select calculate I from the dropdown in the left bottom corner of the calculator window. Now calculated pH is 6.83 - which means that our buffer solution pH (if prepared neglecting ionic strength) will be 0.37 unit off! Note, that 0.1 is a rather low IS value, sea water has ionic strength of about 0.7 and many common lab reagents have much higher ionic strength.
As the activities of ions are function of their concentrations (through ionic strength), calculations have to be done iteratively. In first step you should calculate all concentrations assuming ionic strength of 0 (and all activity coefficients of 1). If some of the reagents obviously dissociated you may already calculate first value of the ionic strength at this stage. After concentrations are known you should use formulas 17.1 and 17.2 to find ionic strength and all activity coefficients and repeat calculations using these values. This gives new set of concentrations and whole process should be repeated until results of calculations doesn't change (or the difference between two steps or calculations is small enough). Remember, that ionic strength is calculated as sum of concentrations, not activities of ions.



