The acid base titration curve calculation.
Titration curve is not different from any other pH calculation - at each titration curve point we have just a water solution of acid and base. Thus we have to start finding out analytical concentrations of both and then calculate equilibrium. We can either use full blown exact approach, or simplified methods derived in other sections of the site. Before getting to simplified methods let's take a look at two possible general approaches, exact - but numerically heavy.
The most obvious approach relies on the methods of the salt pH calculation, and the most important part of the work has been already done in the salt section. Equation 11.13 (or 11.16 in the case of polyprotic acids and bases) describes whole acid-base titration curve, your only task is to calculate Ca and Cb values for any given titration moment and that's a task on a high school level. This is how BATE pH calculator generates acid base titration curves. However, there is also other, interesting approach to exact curve calculation, that doesn't require solving high degree equation.
Let's try it for the simplest case - strong acid titrated with strong base. We assume both acid and base are so strong we can ignore their dissociation constants. If so, the most important equation describing the solution is the charge balance equation:
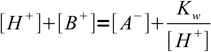 16.1
16.1which is presented here in the version already taking water autodissociation into account. Now let's assume we are titrating Va volume of the acid of Ca concentration with base of Cb concentration. Taking dilution into account we can write
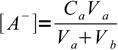 16.2
16.2and
 16.3
16.3(we have assumed 100% dissociation). Once combined these equations yield
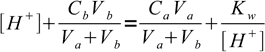 16.4
16.4This equation combines pH, Ca, Cb, Va and Vb. When we want to draw a titration curve we usually know both concentrations of titrant and titrated substance, as well as initial volume of titrated substance. Thus, if we solve equation 16.4 for Vb:
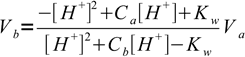 16.5
16.5we will get equation that allows us to calculate volume of titrant that was added to the solution to get given pH. Not every combination of acid and base will yield every possible pH, but it will be obvious, as using pH values from outside of the possible pH range we will get negative volumes of titrant.
Using this equation is a little bit counterintuitive, as to draw a plot we have to switch coordinates and use ordinate as a function argument and abscissa as the function value, but calculations are pretty straightforward.
The same approach can be used to produce much more general equation. To do so we should start with full charge balance equation and use concentrations of acid and base forms calculated using equations derived in the pH of polyprotic acid section (see equations 9.12 and 9.13). However, this was already done to get the equation 11.16, so we can just plug Ca and Cb from equations 16.2 and 16.3 into 11.16 and solve for Vb:
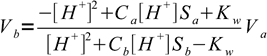 16.6
16.6where
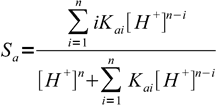 16.7
16.7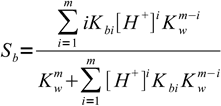 16.8
16.8To use this equation it is enough to plug numbers, so it is much easier to use than it may look at first.
However, if you have to calculate acid-base titration curve by yourself (not using BATE pH calculator or any other program) both approaches are difficult, as they are numerically heavy and equations used are not human calculations friendly. Thus you have to apply some easy methods described in previous sections.
For the titration of strong acid (base) we assume that pH is controlled just by the concentration of the not neutralized titrated substance before end point, and by the excess of titrant after end point. Near the endpoint you may use equation 7.4 to take water dissociation into account, or - if there is no need for so precise pH calculations - you may assume endpoint pH to be 7.00. That's not exactly true, as the strongest bases used are not as strong as acids and the hydrolysis can lower pH by few hundredths, but this effect is negligible.
For the titration of the weak acid (or base) using strong neutralizing agent starting point pH is just pH of weak acid solution (see equation 8.10 or 8.13), acid base titration curve before endpoint is described by Henderson-Hasselbalch equation, for endpoint pH is calculated as for salt solution, further values are calculated from the titrant excess.
Finally for titration of weak acid (base) using weak base (acid) equation 11.13 (or 11.16) must be used. Such titrations are never done in laboratory practice. Calculations are not easy and this is one of the cases when use of some kind of pH calculator is a must.
You may visit www.titrations.info site and especially acid-base titration curve calculation page to see some simple examples of calculation.



