Brønsted-Lowry's acids and bases
Even if acids and bases can exist and react in other solvents, all reactions we are interested in here take place in water, which dissociates itself into H+ and OH- ions. That makes a classic definition of an acid as a substance that dissociates producing H+ ions (the one we used in equation 1.1) a little bit problematic. Consider the solution of salt of a weak base BOH. Such solution contains B+ ions, that are between products of BOH dissociation:
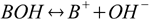
with equilibrium described by the already mentioned in the previous section base dissociation constant:
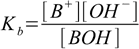 2.1
2.1For the equilibrium BOH molecules are needed. As there are already OH- ions from the water dissociation present in the solution, they will react with B+. This will lower OH- concentration, forcing water to dissociate further. Final solution in equilibrium will contain some BOH molecules and some excess of H+ - so it will be acidic, even if we haven't add any acid! Seems that B+ is an acid - even if it doesn't dissociate to give H+ ions.
To overcome this inconsistency (as well as some other) Brønsted and Lowry proposed independently in 1923 new definitions of acid and base: acid is a substance that can donate the proton and base is a substance than can accept the proton. The most important outcome of this definition is the fact that every acid loosing its proton becomes a Brønsted-Lowry base (as it has a free "slot" for the proton) and that every base when protonated becomes a Brønsted-Lowry acid (it has a proton that is can release). These pairs of acid and base are called conjugate. In other words every acid loosing proton becomes its conjugate base, and every protonated base becomes its conjugate acid.
This approach has some interesting implications. Let's take a reaction of conjugate base A- with water:
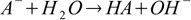
Its equilibrium constant is
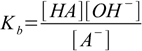 2.2
2.2(water concentration assumed constant). Multiplying this equation by the equation for acid dissociation constant we get
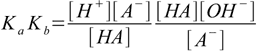 2.3
2.3[A-] and [HA] cancel out leaving
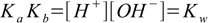 2.4
2.4or
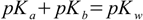 2.5
2.5The most important lesson is that to describe acid/base properties of substance in the solution (not necessarily water solution) we can use either Ka or Kb value. Sometimes it is more convenient to use Kb for calculations, but whenever selection of constant doesn't matter we will concentrate our efforts around Ka according to widely accepted convention.
It is worth of noting here that applicability of the Brønsted Lowry theory extends to other solvents, and that at least some of them are capable of "autodissociation" (or some other reaction between solvent molecules, which is technically equivalent). That means an almost identical math and rules can be applied to describe acid/base equilibria in non-aqueous solvents, it is just out of scope of our lectures.



