Calculation of pH of any salt solution
pH of all salts solutions is determined by the hydrolysis and - in the case of acidic or basic salts - by the dissociation. In case of salts of strong acids and strong bases effects of the hydrolysis are often negligible, but - as it was pointed out earlier - some of the strong acids and bases are weaker than it is commonly believed.
Let's solve the problem for simple salt using general approach.
We have two substances - HA and BOH - and two dissociation constants:
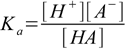 11.1
11.1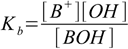 11.2
11.2water dissociation constant:
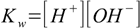 11.3
11.3and three balances:
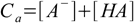 11.4
11.4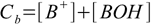 11.5
11.5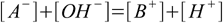 11.6
11.6In the case of salt solution Ca=Cb, but we have a good reason to treat these values separately. Once the general equation will be derived we can always simplify it using only one concentration, but general equation will describe not only pH of the salt solution, but also of any mixture of weak acid and weak base, regardless of their ratio.
In deriving the equation we could use the same approach we tested for polyprotic acid, but we will try shorter way that was not applicable then. We will use dissociation constants and mass balances to find out concentrations of A- and B+ ions to put them into charge balance equation. From acid mass balance:
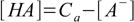 11.7
11.7Inserted into 11.1
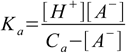 11.8
11.8Solved for [A-]:
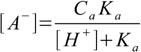 11.9
11.9and ready to be put into charge balance.
Now do the same to the base, using Kb and Kw definition:
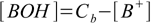 11.10
11.10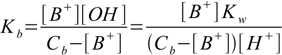 11.11
11.11solving for [B+] yields
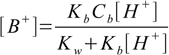 11.12
11.12and finally, combining 11.9 with 11.12 and charge balance we get
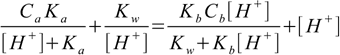 11.13
11.13which is a fourth degree equation for [H+] in any mixture of weak acid and weak base.
Using for calculations
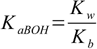 11.14
11.14we get very similar, strikingly symmetrical result:
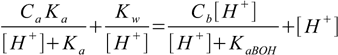 11.15
11.15It is worth of noting here that the equation used for pH calculation in BATE pH calculator is just a full polyprotic version of the 11.13 (note that generalized equation 11.16 uses not stepwise, but overall dissociation constants Kai and Kbi):
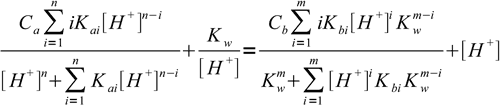 11.16
11.16


