pH lectures - the water ion product
Not only acids and bases dissociate, water dissociates too:
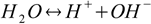
and the equilibrium of this reaction is described by the equation
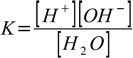 1.7
1.7However, in practice we use simplified version of this equation, called water ionization constant (sometimes called also water ion product)
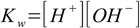 1.4
1.4Why can do we do that? As long as we are talking about diluted solutions we may safely assume water concentration is constant, and error introduced into our calculations will be rarely higher than the precision of dissociation constants used in calculations. K given by the equation 1.7 has a value of 1.8×10-16. We know that there is 1000 g of water per liter and it has a molar mass of 18 g, thus the water concentration is [H2O] = 1000/18 = 55.56 M. If we assume water concentration doesn't change we can rewrite equation 1.7 as
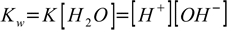 1.8
1.8This new Kw constant will have a value of 1.8×10-16×55.56=10-14. That's why Kw is sometimes listed as 10-14 (pKw=14) and sometimes as 1.8×10-16 (pKw=15.7).
Equation 1.8 is quite often very useful. If we take log of boths sides of the equation (and change the sign) we get
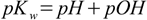 1.6
1.6When dealing with solutions of bases it is usually much easier to calculate concentration of OH- and pOH, equation 1.6 comes very handy then, as it allows to almost effortlessly convert pOH to pH.
For the sake of simplicity we will always use equation 1.4 and we will assume Kw=10-14 (or pKw=14) in all our calculations. In a real world Kw value is highly temperature dependent:
| T (°C) | Kw | pKw | neutral pH |
|---|---|---|---|
| 0 | 0.114 × 10-14 | 14.94 | 7.47 |
| 5 | 0.186 × 10-14 | 14.73 | 7.37 |
| 10 | 0.293 × 10-14 | 14.53 | 7.27 |
| 15 | 0.457 × 10-14 | 14.34 | 7.17 |
| 20 | 0.681 × 10-14 | 14.17 | 7.08 |
| 25 | 1.008 × 10-14 | 14.00 | 7.00 |
| 30 | 1.471 × 10-14 | 13.83 | 6.92 |
| 35 | 2.089 × 10-14 | 13.68 | 6.84 |
| 40 | 2.916 × 10-14 | 13.54 | 6.77 |
| 45 | 4.074 × 10-14 | 13.39 | 6.70 |
| 50 | 5.476 × 10-14 | 13.26 | 6.63 |
| 55 | 7.244 × 10-14 | 13.14 | 6.57 |
| 60 | 9.550 × 10-14 | 13.02 | 6.51 |
| 65 | 12.58 × 10-14 | 12.90 | 6.45 |
| 70 | 15.85 × 10-14 | 12.80 | 6.40 |
| 75 | 20.42 × 10-14 | 12.69 | 6.35 |
| 80 | 25.12 × 10-14 | 12.60 | 6.30 |
| 85 | 30.90 × 10-14 | 12.51 | 6.26 |
| 90 | 38.02 × 10-14 | 12.42 | 6.21 |
| 95 | 45.71 × 10-14 | 12.34 | 6.17 |
| 100 | 51.3 × 10-14 | 12.29 | 6.14 |
It is commonly assumed that neutral solution pH is 7.00. In most cases that's a very good approximation, but - as the water dissociation constant varies with temperature - it is true only for 25 °C. Neutral solution is defined as the one in which concentration of H+ is identical with concentration of OH- and its pH may vary from 7.47 at 0 °C to 6.14 at 100 °C.



