Simplified methods of pH calculation of polyprotic acid/base solution
As every next dissociation constant is smaller usually it is enough to do the pH calculation treating acid as if it was only diprotic (ie omitting effects of the next dissociation step). Further if the acid is weak even in respect to the first dissociation step and the second constants is much smaller, we can neglect second dissociation step completely.
Let's try ascorbic acid with pKa1=4.17, pKa2=11.56:
| Ca (M) | pH calculator | pH eq. 8.10 |
|---|---|---|
| 1 | 2.09 | 2.09 |
| 0.1 | 2.59 | 2.59 |
| 10-4 | 4.26 | 4.26 |
| 10-6 | 6.00 | 6.01 |
| 10-7 | 6.79 | 7.00 |
| 10-8 | 6.98 | 8.00 |
As expected, simplified pH calculation done for only first dissociation step give good results as long as the acid is not too diluted.
Problem arises when the difference between both constants is small or when both dissociations constants are relatively large, but not large enough to treat the acid as dissociated completely for both protons. The second case is especially true for sulfuric acid, with pKa1=-3 and pKa2=2, but it holds also for hypothetic acid with pKa1= 1 and pKa2=2.
Such a case can be solved using interesting approach with two H+ concentrations. Let's call them H1 and H2 respectively. H1 is concentration of H+ from the first dissociation step, H2 - from the second. Total concentration of H+ (the one we will use to determine pH) is H1+H2.
First step is to calculate H1 either using methods for weak acid solution or assuming that first proton is fully dissociated. Now let's take a look at the second dissociation step and the second dissociation constant:
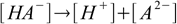 10.1
10.1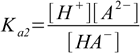 10.2
10.2Before second step of dissociation started
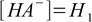 10.3
10.3(as long as the acid is not too diluted and water dissociation can be neglected). After the equilibrium have been reached
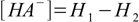 10.4
10.4and
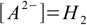 10.5
10.5Of course such splitting of the dissociation into phases is not a thing occurring in reality, it only helps us in formulation of the equations.
Inserting 10.4 and 10.5 into 10.2 we get
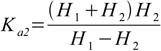 10.6
10.6Note that we used sum H1+H2 in the numerator, as in the dissociation constant total concentration of H+ is used.
Equation 10.6 is quadratic in respect to H2 and both H1 and Ka2 are known. Only one root is positive.
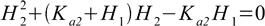 10.7
10.7If second dissociation constant is much lower than the first, H2 in denominator can be further neglected and the equation 10.6 can be simplified even more.
How precise are results of this approach? Let's try them for sulfuric acid first, assuming H1=Ca:
| Ca (M) | pH calculator | H1 (Ca) | H2 (10.7) | pH (H1+H2) |
|---|---|---|---|---|
| 1 | 0.00 | 1 | 9.81×10-3 | 0.00 |
| 0.1 | 0.96 | 0.1 | 8.44×10-3 | 0.96 |
| 0.01 | 1.85 | 0.01 | 4.14×10-3 | 1.85 |
| 0.001 | 2.73 | 0.001 | 8.44×10-4 | 2.73 |
| 10-4 | 3.70 | 10-4 | 9.81×10-5 | 3.70 |
| 10-5 | 4.70 | 10-5 | 9.98×10-6 | 4.70 |
| 10-6 | 5.70 | 10-6 | 1.00×10-6 | 5.70 |
| 10-7 | 6.62 | 10-7 | 1.00×10-7 | 6.70 |
| 10-8 | 6.96 | 10-8 | 1.00×10-8 | 7.70 |
Looks pretty good, isn't it? Problems start when the solution is pretty diluted - below 10-6 M. It seems also that for solutions below 10-3 M you may safely assume both protons of sulfuric acid are fully dissociated.
And what about our second acid, the one with pKa1=1 and pKa2=2? First dissociation step is too weak for H1=Ca assumption to hold and too strong for simplified equation 8.13. Thus we will use equation 8.10.
| Ca (M) | pH calculator | H1 (8.10) | H2 (10.7) | pH (H1+H2) |
|---|---|---|---|---|
| 1 | 0.55 | 0.270 | 9.33×10-3 | 0.55 |
| 0.1 | 1.16 | 0.0618 | 7.77×10-3 | 1.16 |
| 0.01 | 1.88 | 9.16×10-3 | 3.96×10-3 | 1.88 |
| 0.001 | 2.74 | 9.90×10-4 | 8.37×10-4 | 2.74 |
| 10-4 | 3.70 | 9.99×10-5 | 9.80×10-5 | 3.70 |
| 10-5 | 4.70 | 1.00×10-5 | 9.98×10-6 | 4.70 |
| 10-6 | 5.70 | 1.00×10-6 | 1.00×10-6 | 5.70 |
| 10-7 | 6.62 | 1.00×10-7 | 1.00×10-7 | 6.70 |
| 10-8 | 6.96 | 1.00×10-8 | 1.00×10-8 | 7.70 |
Once again results are perfect as long as the water dissociation doesn't enter the scene.
What is important here is the fact, that using equation 10.7 for the ascorbic acid, the one from the beginning of the section, we will get proper results too - just the pH calculation will be overdone.
It is interesting to note, that if the difference between dissocation constants is large enough so that only first dissociation step is responsible for pH, concentration of A2- is numerically identical with Ka2. That's pretty easy to show - just solve second dissociation constant for [A2-]:
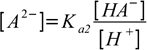 10.8
10.8As all H+ are assumed to be from first dissociation step, [HA-]=[H+]. Thus concentrations on the right side of the equation cancel out and we are left with [A2-]=Ka2

