Newton method for numerical finding of function roots
Newton method is used for numerical solving of non-linear equations given in the form
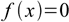 18.1
18.1To be able to solve the equation we must know its first derivative f'(x) (or we must be able to differentiate function numerically). As all functions we are interested in in pH calculations can be converted to polynomial forms we can assume that we know f'(x). Newton method of solving the equation (18.1) uses iterative formula:
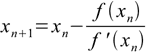 18.2
18.2The problem is nth degree polynomial can have n different roots of which only one has chemical sense. To find it we have to select good value for x0. In case of acids good starting value is concentration of H+ ions calculated with assumption of full dissociation of all protons.
Iterations are done until the difference between xn+1 and xn gets smaller than the predefined treshold.
In case of polynomials having real roots Newton method is always convergent.



