Buffer lectures - calculation of pH change after addition of a strong acid/base
Apart from calculations needed for buffer preparation, we are often interested in the change of the pH after some amount of a strong acid or strong base was added to the buffered solution. Buffer capacity, which we will discuss on the next page, allows us to compare resistance of buffers to pH changes, but doesn't give an exact answer to the question "by how much pH will change". This has to be calculated - and calculations don't require any new methods but the ones we have already used.
By how much will the pH of 100 mL of 0.1 M acetic buffer at pH=4.75 change after addition of 0.0005 moles of HCl?
When we add strong acid to acetic buffer, we protonate the conjugate base (Acetate-), producing the weak acid HAcetate. As usual, we will do the calculations assuming reaction is stoichiometric and exactly 0.001 moles of base is converted to the conjugate acid.
First, we need to calculate concentrations of acetic acid and acetate, but in this particular case answer is pretty obvious and immediately follows from the Henderson-Hasselbalch equation:
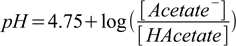 4.1
4.1pH=pKa, so the log part is zero, which in turn means ratio of concentrations equals 1 and they are identical. As their sum is 0.1 M they have to be both 0.05 M. It won't be that easy in the next question.
As we have 100 mL of the solution at 0.05 M, there is 0.005 moles of acetic acid and 0.005 moles of acetate. After adding 0.0005 moles of HCl amount of acid grows to 0.0055 moles, while the amount of conjugate base goes down to 0.0045 moles. We have already seen earlier that Henderson-Hasselbalch equation holds not only when we plug in concentrations, we can also plug in numbers of moles of acid and conjugate base, as the volume cancels out. That means we can write
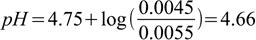 4.2
4.2And the final answer is - pH changed by 4.66-4.75=-0.09 pH unit.
By how much will the pH of 0.1 M acetic buffer at pH=5.75 change after addition of 0.0005 moles of NaOH?
While in many aspects this question is almost identical, we can't start it that easily, as pH is quite different from pKa. But we know how to start - first of all, we will calculate ratio of concentrations of acetic acid and acetate:
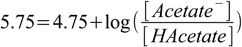 4.3
4.3or:
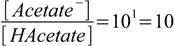 4.4
4.4And we know
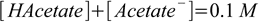 4.5
4.5so we have two equations in two unknowns, when solved they give
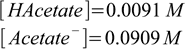 4.6
4.6There is 0.1 L of the buffer solution, so numbers of moles are respectively 0.00091 (HAcetate) and 0.00909 (Acetate-). After adding 0.0005 moles of strong base number of moles of HAcetate becomes 0.00091-0.0005=0.00041, and number of moles of acetate grows to 0.00909+0.0005=0.00959. Plugging these values into Henderson-Hasselbalch equation we get
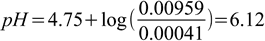 4.7
4.7so the pH changed this time by 6.11-5.75=0.36.
Have you noticed, that in both cases we added the same amount of a substance to change pH of the buffer, yet the answer was quite different? pH of the first buffer changed just by 0.09 unit, while the pH of the second changed by 0.36 - change was four times as large. Why? Well, it was already signaled earlier, that buffers are most effective when concentrations of both acid and conjugate base are almost identical - that happens when pH is close to the acid pKa. First buffer had pH=pKa, so it was the best possible buffer for that pH. Second buffer had pH that was 1 pH unit from the pKa (which is usually considered the maximum acceptable distance) and its resistance to pH changes was much lower.



