Buffer lectures - introduction

pH of the solution impacts all reactions taking place in water. Sometimes the effect is pretty easy to observe (permanganate is a strong oxidizing agent, but depending on the solution pH it gets reduced to manganate, manganese(IV) oxide or Mn(II)), sometimes the effect of pH is less pronounced and can be ignored for all practical purposes, (BaSO₄ solubility at pH 1 is about ten times higher than at pH 7, but the solid precipitates even in highly acidic solutions), but it is present always. This is especially important in the case of biochemical systems. Most of the molecules involved in a typical biochemical process are weak acids or bases (often both, with multiple functional groups), depending on pH they get protonated or deprotonated, which usually means their properties change. That in turns modifies fragile equilibria and kinetics of reactions in which these molecules are involved and in effect shift of pH even just by less than a tenth pH unit can completely change the reaction products, rendering reaction pathway useless. This can be lethal for the living organisms, but it also means when researching biochemical processes in vitro we need to be able to control pH with a high precision - otherwise our results are likely to be irreproducible.

Note, that controlling pH is not only about preparing solution of known pH, it is also about being able to maintain a constant pH. Quite often reactions produce or consume H⁺ (OH^-) ions, which in turn leads to pH change. Neutral water contains 10^-7 M of H⁺, which means that just producing 10^-5 moles of H⁺ per liter changes the pH by two units. Mass of the 10^-5 moles of a typical substance is in the mg range - we are talking about a single crystal of sucrose dissolved in 1 L of water (single digit ppm concentration). Make the volume 1 mL, and the amount of substance that can change pH by two units by producing or consuming H⁺ becomes too small to be visible as a solid.

Luckily, keeping pH under control is not that difficult. When the solution contains about equal amounts of acid and its conjugate base - like acetic acid and acetate, or carbonate and bicarbonate, or ammonia and ammonium cation - small amounts of H⁺ produced (or consumed) will just slightly change concentrations of the conjugate pair, and the pH will remain almost constant.

Let's see, if we can show that using a little bit more rigorous approach. Let's assume we have a solution of a weak acid HA, with a conjugate base A-, and the dissociation reaction is

HA ↔ H⁺ + A^-

Dissociation constant K_a for this reaction is

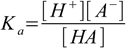1.1

We can slightly rearrange the equation, and express concentration of H⁺ as a function of the [HA]/[A^-] ratio:

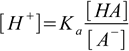1.2

or, after taking logarithms of both sides and doing some sign juggling

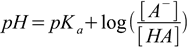1.3

Now, lets assume we have a solution that contains about equal amounts of the acid and its conjugate base - in other words, acid is neutralized in about 50%. If we add some strong acid, it will shift the dissociation equilibrium to the left, and the pH of the solution will go down, but not by much - as the pH depends on the logarithm of the ratio of the concentrations, its changes are quite slow! We call such solutions resisting pH changes pH buffers.

The equation above is called a Henderson-Hasselbalch equation and is widely used in buffer calculations, both to calculate recipes and to predict pH changes.

As adding H⁺ or OH^- to the buffer solution changes concentrations of both acid and its conjugate base, it is important to at least initially keep them close to equal. Why? Let's see what happens when we add some amount of a strong base to the solution of acetic buffer. Let's assume we have a 1 L of a buffer prepared by mixing acetic acid and acetate in the solution, and that their concentrations are both are both 1 M. Plugging these concentrations into Henderson-Hasselbalch equation we will find pH=pK_a. Now, if we add 0.01 moles of a strong base, we will neutralize 0.01 moles of acetic acid, producing additional 0.01 moles of acetate. New ratio of concentrations will be 1.01/0.99=1.02 - still quite close to 1, so the pH didn't change by much (actually by log(1.02)=0.0086 pH unit). But if we start with the initial concentrations of 0.02 M of acetic acid and 1.98 M of acetate (concentration ratio of 1.98/0.02=99), adding the same 0.01 moles of NaOH will change concentrations to 1.99 and 0.01 and the ratio will become 1.99/0.01=199 - twofold change, which leads to a much larger pH change (0.3 pH unit)! Resistance of the buffer to the pH changes is called buffer capacity and is the largest when pH=pK_a. We will discuss it in more details later, for now let's remember as a rule of thumb that when selecting the acid for the buffer we should always select one that has pK_a within one unit from the planned pH.

An important thing to remember, and the one that is surprisingly often missed by people just starting to learn about buffers, is that when we talk about the acid and the base that make the buffer we are talking about conjugate pair - so for example in the acetic buffer base is not NaOH used to neutralize the acid, but the Acetate^- ion (please read on Brønsted-Lowry acid theory, if you have problems understanding the idea). It happens that often amount of the strong base used for neutralization is identical to the amount of the conjugate base present in the buffer solution, which just adds to the confusion, but it is not the same thing.