Buffer lectures - thermodynamic corrections, ionic strength
Even ions that don't chemically react in the solution interact physically - they are charged, so they either attract or repel each other and their motions are not completely independent. In the effect presence of other ions always interferes and changes the ion behavior. The higher the concentration of ions, the higher the discrepancy between the real and ideal behavior of the ions. As in typical equilibrium calculations we assume ideal behavior of the ions, the higher the concentration, the higher the difference between observed reality and results of our calculations. Sadly, these differences are observable even in solutions in the range 0.001 M, and in the case of 0.1 M solutions they can't be ignored.
The most often used theory that treats discrepancies between ideal and real solutions is the Debye-Hückel theory, proposed in 1923. Lets assume we have a solution containing several ions, with concentrations c and charge z. In all equilibrium formulas we replace concentrations of ions with their activities, calculated by multiplying concentrations by activity coefficients:
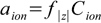 6.1
6.1where aion is the ion activity and f|z| is the activity coefficient of an ion with a charge z (regardless of whether the charge is positive or negative).
For ideal solution the activity coefficient equals 1, for non-ideal solutions it is calculated as a function of ionic strength, defined as
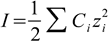 6.2
6.2Ionic strength is a collective parameter, describing presence of all ions in the solution (hence we sum over all ions present). Knowing ionic strength we calculate logarithm of activity coefficients from the formula
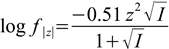 6.3
6.3(activity coefficients for all ions of the same charge are assumed to be identical; in more precise versions of the formula they are also a function of the ionic radius).
Debye-Hückel theory works reasonably well for solutions with ionic strength below 0.1. Despite over 100 years of research we still don't have a good and easy to use theory that would allow correct calculations of ion activities for every solution. There are several extensions to Debye-Hückel theory that use experimentally determined equations and/or parameters, some of them work even for ionic strengths up to 5 or 6. However, they are difficult to use, as they require extensive tables of interaction coefficients for all ion pairs present in the solution, and number of these interaction coefficients measured and published in literature is relatively small. Solution of ammonium hydrogenphosphate, containing 8 different ions/molecules, requires 28 coefficients - some of them can be ignored, as concentrations of some ions are very low, still, (NH4)2HPO4 solution is quite simple compared with blood or sea water.
Despite the fact we don't have good theory allowing calculation of activity coefficients from the first principles, Debye-Hückel theory suggests a convenient way of dealing with corrections to ideal solution behavior. We can write acid dissociation constant as
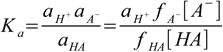 6.4
6.4where ax is activity of ion/molecule x, and fx is its activity coefficient. We left aH+ untouched, as in fact we are interested in the H+ activity, not in H+ concentration (despite the fact pH is often listed as -log([H+]) it is in fact minus logarithm and of the H+ activity, and it is the latter that is measured by pH electrodes or induces color changes of the indicators). If we move now activity coefficient to the LHS of the equation, we will get
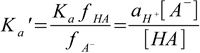 6.5
6.5Ka' is known as a mixed, or practical dissociation constant. Despite the fact it looks a little bit strange, it is very useful, as it can be determined experimentally for a given ionic strength, and then used in calculations mixing pH (activity) and concentrations of the acid and conjugate base. This way we can solve any buffer problem using exactly the same approach we used earlier, and all corrections related to the ionic strength of the solution will be taken care of automatically.
Sometimes also concentrations constant are used, in which all activity coefficients are moved into the dissociation constant value (so we can easily use these constants to calculate concentration of H+, but not its activity). These are quite useful in finding the equilibrium, as mass and charge balance require real concentrations, not activities, and using concentration constants makes it easier to systematically approach the calculations. Unfortunately, it is not always clear what kind of constants is listed in the published tables.
However, to make sure our calculations are correct, we need to make sure ionic strength of the solution we are working with is the one for which we have the value of the practical dissociation constant. Sometimes it requires additional effort when preparing buffer solution. See next page for details on how to keep ionic strength under control.



