How Buffer Maker calculates pH of the solution and buffer composition

Buffer Maker is built around powerful pH calculation engine, capable of dealing with mixtures containing any number of acids. In the program each buffer is prepared mixing two reagents. Buffer Maker starts calculating pH of solutions prepared using individual reagents (diluted as needed). This gives lower and upper interval boundaries, then bisection method is used to find such mixture of reagents that gives required pH.

pH calculation engine is built around charge balance equation. Each solution must be electrically neutral, so if we write equation that combines charge balance with H⁺ concentration and if we solve it - we know what the solution pH is. It can be relatively easy shown that for each acid charge of its dissociation products other than H⁺ is

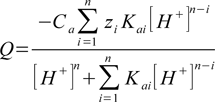
where

• Q - total charge of all forms
• C_a - analytical concentration of acid
• n - number of dissociation steps
• z_i - charge of i^th form produced in dissociation
• K_ai - i^th overall dissociation constant
• [H⁺] - H⁺ concentration

(see our lecture on pH of salt for more details about the equation derivation; note that to simplify calculations we treat here all substances as Brønsted-Lowry acids). Total charge balance equation is

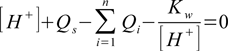
where Q_s is spectators charge and K_w is water ion product. Spectators are ions present in the solution, assumed to not take place in any reactions that consume or produce H⁺ and OH^-.

This equation can be easily solved numerically using Newton method, giving exact pH of the solution regardless of the number of acids present. To make user interface usable Buffer Maker limits number of dissociation steps to 4, this is in most cases enough.

Equations above use just concentrations, for obvious reasons calculations are corrected for thermodynamic effects. To do so K_ai constants are thermodynamically corrected in each iteration. To calculate activity coefficients we use approximate Davies equation (based on extended Debye-Hückel theory)

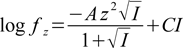
C parameter value doesn't have a generally accepted value and different authors suggest different values from the -0.2 < C < -0.5 interval. Also maximum ionic strength at which Davies equation can be used is listed sometimes as 0.3 and sometimes as 0.5. Buffer Maker allows you to change the default values used by the program. Whenever calculated ionic strength is higher than preset limit, program will display warning - either as a comment to the calculation results, or displaying ionic strength in color. This is described in appropriate places in the help.

K_a is corrected not only for thermodynamic effect, but also - whenever data is available - for thermal effects. New K_a values are calculated using linear correction and dpK_a/dT values.

Both K_w and A values are assumed to be functions of temperature. To find K_w program uses tabularized values (identical to those listed on our water ion product page), doing linear interpolation between data points. For a given temperature T (deg C) A is calculated as

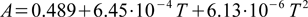
Buffer capacity is calculated by numerical differentiation of pH calculated using above method, and on some rare occasions spikes can appear on the plot - these are usually effects of the rounding errors and can be safely ignored.

It may be worth of noting here, that model used - while limited - is much more flexible and gives much better results, than calculations based on Henderson-Hasselbalch equation. For example numerous buffer calculation scripts present on the web use Henderson-Hasselbalch equation to calculate composition of 0.01M chloroacetate buffer pH=2.33. This is just about 0.55 pH unit from the acid pKa, so may seem correct - but it is not. Pure 0.01M chloroacetic acid has pH 2.52, so such a buffer cannot be prepared. If you will decide to follow the recipe, your buffer will have pH 2.71. Such things will never happen with Buffer Maker.