Calculate pH of 0.01M aniline hydrochloride. Aniline pKb=9.4.
Aniline in solution of its hydrochloride is in form of conjugate acid. To calculate pH of such solution we have to find pKa for aniline and treat it like weak acid.
Knowing pKb we can find pKa from the equation 2.5:
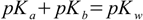 2.5
2.5pKa=14-9.4=4.6 - and this value we will put into simplified formula 8.13.
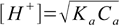 8.13
8.13Result is [H+]=5.0×10-4 M and pH=3.30. We have used simplified formula, so now we have to check if the 5% rule is obeyed:
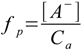 1.3
1.3Dissociation fraction is 5.0×10-4/0.01 - exactly 5%. We were allowed to use equation 8.13.
Our pH calculator doesn't calculate pH for salts, but salt is nothing else but equimolar solution of acid and base. BATE calculates pH as 3.31 - where is the source of difference?
First suspect is 5% rule - it doesn't state results will be exact, but the error will be acceptable. Let's try to calculate the result using more precise formula 8.10.
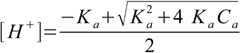 8.10
8.10This time [H+]=4.89×10-4 and pH=3.31. This result is more precise - but is it better and worth additional calculations?
No!
Dissociation constant is given only with two significant digits accuracy, so our pH is in fact 3.3 - or even just 3, as the concentration is given with only one significant digit.
pH calculator always calculate the result with full precision - that's what computers are for. It is up to us - humans - to understand the results.



