Stoichiometric ratio
Stoichiometric calculations based on ratio and proportions are very intuitive, but for some reasons not taught in the US. The general idea was already signaled in the stoichiometric calculations section - ratio of amounts of reagents is always the same and is described by the balanced reaction equation.
Let's take a look at aluminum oxide synthesis:
4Al + 3O2 → 2Al2O3
4 moles of Al react with 3 moles of oxygen, producing 2 moles of Al2O3. If we take 2 moles (instead of 4) of Al we will get only half the product - so there will be only 1 mole of Al2O3 produced. We can write the reaction equation together with amounts of substances (writing amounts of substances below their formulas):
| 4Al | + | 3O2 | → | 2Al2O3 |
| 4 moles | : | 2 moles | ||
| 2 moles | : | x moles |
In the upper line we wrote down what we know from the balanced reaction equation (4 moles of aluminum are used to produce 2 moles of aluminum oxide), in the lower line we wrote the known amount of substance (2 moles of aluminum) and unknown - x moles below aluminum oxide. As we know that the ratio of amounts is always the same, we can write the following proportion:
4 moles : 2 moles = 2 moles : x moles
which reads: ratio of 4 moles of Al to 2 moles of Al2O3 is identical as ratio of 2 moles of Al to x moles of Al2O3. Solving for x (using product of extremes equals the product of the means rule) is very simple:
4x = 2×2
and x = 1 - so we will get 1 mole of Al2O3 (which is hardly surprising).
And how much oxygen will react with two moles of Al?
| 4Al | + | 3O2 | → | 2Al2O3 |
| 4 moles | : | 3 moles | ||
| 2 moles | : | x moles |
This time our ratio looks like that:
4 moles : 3 moles = 2 moles : x moles
using the same rule to solve the proportion again we get
4x = 6
and x = 1.5 mole. We need 1.5 mole of oxygen to fully react with 2 moles of Al.
So far we did calculations using moles, but - and here comes the really useful part - we can use masses as well. Just replace number of moles by mass of these moles - multiplying molar masses by reaction coefficients.
So for example let's try to dissolve 5.00 grams of calcium carbonate in hydrochloric acid and find out how much carbon dioxide was produced. This time we will write under the reaction not number of moles, but molar masses (multiplied by stoichiometric coefficient whenever different from 1):
| CaCO3 | + | 2HCl | → | CaCl2 | + | H2O | + | CO2 |
| 100.1 g | : | 44.01 g | ||||||
| 5.00 g | : | x g |
Our ratio looks this way:
100.1 g : 44.01 g = 5.00 g : x
and x = 44.01 g/100.1 g×5.00 g = 2.20 g
And how much hydrogen chloride is needed to produce 10.00 g of calcium chloride? Nothing easier:
| CaCO3 | + | 2HCl | → | CaCl2 | + | H2O | + | CO2 |
| 2×36.46 g | : | 111.0 g | ||||||
| x g | : | 10.00 g |
2×36.46 g : 111.0 g = x g : 10.0 g
x = 2×36.46 g/111.0 g×10.0 g = 6.57 g
This is really fast and simple, and what is probably most important - once you will get some experience you will start to 'feel' reactions, which helps locate wrong calculation results or estimate amounts of substances in reactions without long calculations. If you know molar masses you basically need one multiplication and one division to solve every stoichiometric problem (well, you need to multiply molar mass by stoichiometric coefficients, so technically there is more to do, but multiplication by small integers is not something difficult enough to mention).
Product of Extremes Equals the Product of the Means:
Proportions can be easily solved using basic algebra - in the worst case you need two steps to solve for the unknown variable. However, there are simple tricks that can speed up the process.
First of all, there is a very useful and easy to remember rule - product of terms on the outside (extremes) equals product of terms close to the equals sign (means):
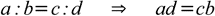
While above rule is widely known and used, you may find the second method of remembering the same rule easier - just follow the red dotted line to recall order of terms:
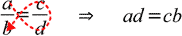
Don't use simplified rules if you don't know how to solve the proportions algebraically.



