program calculating pH - Base Acid Titration and Equilibria - finding equilibrium
For a detailed discussion on methods of calculating pH and for the outline of derivation of the formula displayed below check out our lectures on pH calculation (more specifically calculating pH of a salt solution section).
Calculating pH BATE calculates equilibrium state of mixture of acid and base and pH of this mixture always in the same manner.
Solution containing mixture of acid and base is described by a set of equations:
- acid number of moles balance,
- base number of moles balance,
- charge balance,
- acid dissociation equilibria (one for every step of dissociation),
- base dissociation equilibria (one for every step of dissociation),
- water ionization constant.
As we need method of calculating pH we can combine all these equations into one, containing only constants and H+ concentration:
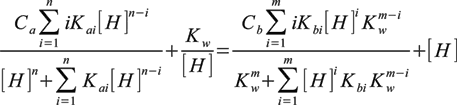
Here m is a number of base dissociation steps and n number of acid dissociation steps. Ka and Kb are overall dissociation constants for acid and base respectively, Kw is water ionization constant. Ca and Cb are analytical (total) concentrations of acid and base.
This equation can be rearranged into polynomial form, which is rather easily solved numerically using Newton method. Calculating pH we could also try to numerically solve full set of equations - but approach used gives faster code at the price of additional work done when deriving above equation.
For the titration curves concentrations of titrant and titrated substance (Ca and Cb) are first calculated for every curve point taking volume changes into account. Then program starts calculating pH for every curve point in usual way.
Debye-Hückel equation
Calculating pH we have to remember about its thermodynamic definition - minus log of H+ activity. To calculate activities of ions we use Debye-Hückel theory. Ionic strength is defined as:
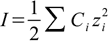
The activity coefficients are calculated as:
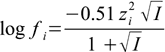
where Ci and zi are concentration and charge of ith ion present in the solution.
Calculations of ionic strength and activity coefficients are done iteratively, using concentrations of all ion forms calculated as a function of [H3O+].



