Dimensional analysis
Dimensional analysis is performed in four steps:
- Find out what is given and what you need to calculate.
- Find out conversion factors needed to convert one value to another. All conversion factors combine numbers and units, and they show what is equivalent to what (like 1 mole of calcium chloride is equivalent to calcium chloride mass of 110.984 g).
- Arrange given information together with conversion factors in such a way, that units in conversion factors cancel out. You must arrange them in such a way that units for the given quantity are present in the denominator of the first conversion factor, while units of the desired quantity are in the nominator of the last conversion factor.
- Calculate.
Let's try this method for some simple question, like how much magnesium oxide will be produced if 3.000 g of magnesium ribbon is burnt in the air. Balanced reaction equation is:
2Mg + O2 → 2MgO
Our given information is mass of magnesium - grams of Mg. We are looking for grams of magnesium oxide - grams of MgO. Note, that units used (grams of Mg and grams of MgO) are combinations of mass and substance - that's very important.
We can solve the question with three conversions:
grams of Mg → moles of Mg → moles of MgO → grams of MgO
First conversion factor is based on the magnesium molar mass:
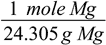
Second is based on the stoichiometry given by the reaction equation:

And the third one is similar to the first one, but involves MgO and its molar mass:
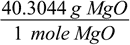
When properly arranged all units cancel out, and after calculations we are left with the final result:
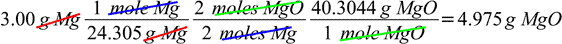
But there is also a shorter way possible, with only one conversion, given by the ratio of MgO mass produced in the reaction, to the mass of Mg entering the reaction:
grams of Mg → grams of MgO
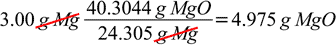
The most important conversion factor in both cases is molar (or mass) ratio taken from the balanced reaction equation. As we are using ratio in calculations - we can as well use the ratio method from the very beginning, although dimensional analysis approach should be much safer if used consistently throughout whole calculation process.
It is worth of noting here that dimensional analysis can be used also for many other types of conversions - like mass/gas volume, volume units (mL → L), length units (cm → inches), some concentration units, and so on. While all these conversions can be done by other means, dimensional analysis is a one tool covering many needs, thus it is worth knowing.
The main problem with dimensional analysis is that it is way too often used without consistency and understanding, which ends in a series of multiplications by randomly selected conversion factors, in a hope that the guess will be correct. It rarely is.



