Calculate the pH of a 0.2M solution of ammonia. Ka=5.62×10-10.
Ammonia is a weak base, so the most convenient approach is to calculate pOH using Kb, and then to convert it to pH.
From the Brønsted-Lowry theory we know that Ka×Kb=Kw, that allows us to calculate Kb=Kw/Ka=10-14/5.62×10-10=1.78×10-5.
Calculation of the pOH will be now identical with the calculation of pH of a weak acid.
Let's try first with the simplified formula 8.17:
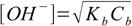 8.17
8.17If we put concentration and Kb values into formula we get [OH+]=0.00189 M and pOH=2.72. Is it correct? To be sure we have to check if the 5% rule is obeyed, that is if the dissociation fraction is less than 5%.
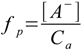 1.3
1.3Dissociated base concentration is the same as [OH-] - if we assume that we can neglect water dissociation. It is obvious that we can, as 0.00189 M is about five orders of magnitude larger than the concentration of OH- from the water. So dissociation fraction is 0.00189/0.2 - below 1%, much less than 5%, so the 5% rule is obeyed.
Now we need the final touch - we know pOH=2.72, but we need pH. Time to use equation 1.6. pH=14-2.72=11.28.
Our pH calculator shows 11.27. Difference in the last digit can be probably attributed to different dissociation constant used.



