Buffers and the derivation of the Henderson-Hasselbalch equation
Solutions able to retain a constant pH regardless of small amounts of acids or bases added are called buffers. Classical buffer contains both a weak acid and its conjugate base. Small amounts of acids or bases added are absorbed by the buffer and the pH changes only slightly. In the case of high or low pH just solutions of strong acids or bases are used - for example in the case of pH=1 acid concentration is relatively high (0.1 M) and small addition of acid or base doesn't change pH of such solution significantly.
How to calculate the pH of a buffer solution containing both acid and conjugate base? Dissociation constant definition 1.1 can be rearranged into
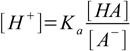 15.1
15.1or
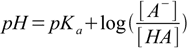 15.2
15.2(note that due to sign change [A-] was moved to nominator).
This is so called Henderson-Hasselbalch equation (or a buffer equation). It can be used for pH calculation of a solution containing pair of acid and conjugate base - like HA/A-, HA-/A2- or B+/BOH. For solutions of a weak bases sometimes it is more convenient to use equation in the form
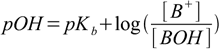 15.3
15.3Both equations are perfectly equivalent and interchangeable.
The Henderson-Hasselbalch equation is used mostly to calculate pH of solutions created mixing known amounts of acids and conjugate bases (or neutralizing part of acid with a strong base). For example, what is the pH of a solution prepared mixing reagents so that it contains 0.1 M of acetic acid and 0.05 M NaOH? Half of the acid is neutralized, so concentrations of acid and conjugate base are identical, thus the quotient under logarithm is 1, the logarithm is 0 and pH=pKa.
This approach - while perfectly justifiable in many cases - is dangerous, as it creates false conviction that the equation can be used this way always. That's not true.
The Henderson-Hasselbalch equation is valid when it contains equilibrium concentrations of an acid and a conjugate base. In the case of solutions containing not-so-weak acids (or not-so-weak bases) equilibrium concentrations can be far from those predicted by the neutralization stoichiometry.
Let's replace the acetic acid from our example with something stronger - e.g. dichloroacetic acid, with pKa=1.5. Repeating the same resoning we used earlier we will arrive at pH=1.5 - which is wrong. The proper pH value can be calculated from the equation 11.13 or using the pH calculator - and it is 1.78. The reason is simple. The dichloroacetic acid is strong enough to dissociate on its own and equilibrium concentrations of the acid and conjugate base are not 0.05 M (as we expected from the neutralization reaction stoichiometry) but 0.0334 M and 0.0666 M respectively.
As a rule of thumb you may remember that acids with pKa below 2.5 dissociate too easily and use of the Henderson-Hasselbalch equation for pH prediction can give wrong results, especially in the case of diluted solutions. For solutions above 10 mM and acids weaker than pKa>=2.5, the Henderson-Hasselbalch equation gives results with acceptable error. The same holds for bases with pKb>=2.5. However, the same equation will work perfectly regardless of the pKa value if you are asked to calculate a ratio of the acid to conjugate base in the solution with a known pH.
Similar problem is present in the calculation of pH of diluted buffers. Let's see what happens when you dilute acetic buffer 50/50:
| Ca (M) | buffer pH found with the pH calculator |
|---|---|
| 0.1 | 4.76 |
| 0.01 | 4.76 |
| 10-3 | 4.79 |
| 10-4 | 4.95 |
| 10-5 | 5.47 |
| 10-6 | 6.31 |
| 10-7 | 6.89 |
The more diluted the solution is, the more solution pH is dominated not by the presence of acetic acid and its conjugate base, but by the water autodissociation. The pH of 1 mM solution is close enough to the expected (from pKa) value, more diluted solutions deviate more and more. It is worth of noting here that 1 mM buffer solution has so low capacity, that it has very limited practical use.
The Henderson-Hasselbalch equation can be also used in the case of polyprotic acids, as long as the consecutive pKa values differ by at least 2 (better 3). Thus it can be safely used in the case of phosphoric buffers (pKa1=2.148, pKa2=7.199, pKa3=12.35), but not in the case of citric acid (pKa1=3.128, pKa2=4.761, pKa3=6.396). In the latter case to calculate pH you should use full equation 11.16 - or the pH calculator.
If you are looking for a way to calculate buffer composition, you can reverse the equation. Using known pH and known pKa you can calculate the ratio of concentrations of the acid and conjugate base, necessary to prepare the buffer. Further calculations depend on the way you want to prepare the buffer. You will find several examples of buffer composition calculations at buffer lectures.
Note: if you need program that will help in buffer calculation, you can try our Buffer Maker - the ultimate buffer calculator.



