Calculation of pH of amphiprotic salt solution
Another interesting case worth of addressing here is calculation of pH for amphiprotic substance HA-, present in the solution of acidic salts. The problem is, HA- hydrolyses and dissociates at the same time and it is not obvious which of these processes will be be responsible for the final pH, moreover, it is very likely that pH can be attributed to some equilibrium between both reactions.
Using the most general approach we would start from the full set of equations. Let's simplify this situation assuming that water ionization can be neglected, and all equations we have to use are these for Ka1, Ka2 and mass balance:
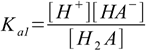 12.1
12.1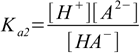 12.2
12.2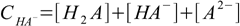 12.3
12.3CHA- is the concentration of the source of the amphiprotic substance - for example of the NaHA salt.
H+ ions are produced in the dissociation reaction (together with A2-) and consumed in the hydrolysis (yielding H2A), so their concentration is:
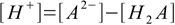 12.4
12.4Using 12.1 and 12.2 we can rewrite 12.4 in the form:
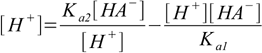 12.5
12.5or, after rearranging:
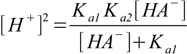 12.6
12.6It is time for two more assumptions. First of all, let's assume that neither dissociation nor hydrolysis goes too far, and [HA-] = CHA-. If so
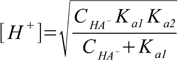 12.7
12.7Now, let's look at the denominator - if the CHA- is sufficiently larger than Ka1 we can neglect Ka1 and whole equation takes form
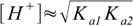 12.8
12.8or
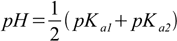 12.9
12.9Interestingly, we can find the same result calculating Ka1Ka2 product:
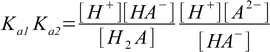 12.10
12.10Canceling out we get
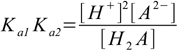 12.11
12.11or
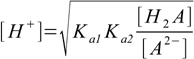 12.12
12.12Comparing 12.8 and 12.12 it is obvious that both assumptions that allowed to derive equation 12.8 are equivalent to the assumption that quotient [H2A]/[A2-] is close to 1.
How precise is equation 12.8?
For NaH2PO4 (pKa1=2.148, pKa2=7.199, pKa3=12.35) results of pH calculation are as follows:
| C (M) | pH calculator | pH eq. 12.8 |
|---|---|---|
| 1 | 4.68 | 4.67 |
| 0.1 | 4.69 | 4.67 |
| 0.01 | 4.79 | 4.67 |
| 0.001 | 5.13 | 4.67 |
When the salt concentration reaches 0.01M it starts to be comparable with Ka1 and denominator from the equation 12.7 can't be simplified by omitting Ka1.
For Na2HPO4 we can additionally assume that first dissociation constant is so large (compared to Ka2 and Ka3) that we can neglect its effects and calculate pH as 1/2(pKa2+pKa3) (treating acid as diprotic):
| C (M) | pH calculator | pH eq. 12.8 |
|---|---|---|
| 1 | 9.76 | 9.77 |
| 0.1 | 9.72 | 9.77 |
| 0.01 | 9.51 | 9.77 |
| 0.001 | 9.09 | 9.77 |
This time we are getting hit by omitted water dissociation, but for solutions above 0.01M results are acceptable.



