Buffer lectures - composition calculation
Buffer calculations - when the pH is within one unit from pKa - are almost always based on the Henderson-Hasselbalch equation and assumption that concentrations of acid and its conjugate base are those given in the question, or just those calculated from the neutralization stoichiometry (in other words, there is no need to calculate exact equilibrium). For example when the question is
What is pH of the solution prepared by mixing 50 mL of 0.01 M acetic acid and 50 mL of 0.01 M sodium acetate?
we will simply assume concentrations of the acid and conjugate base to be identical, thus their ratio is
 2.1
2.1and after plugging it into the Henderson-Hasselbalch equation
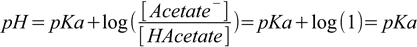 2.2
2.2we have pH=pKa (which we will assume to be 4.75 for the acetic acid). Exact calculations (see the ICE table approach, or use any other method or our pH calculators) show that in reality acid dissociates a little bit, and the ratio of [HAcetate]/[Acetate-] is 4.98×10-3/5.02×10-3=0.992 - slightly lower than 1. Technically our result is guaranteed to be slightly incorrect, but as we rarely know concentrations and Ka values with high accuracy, it doesn't make sense to waste time to improve the result be several tenths of percent.
Such an approach works pretty nicely for every buffer solution that is not too diluted (10 mM at least) and for pH and pKa between 4-10. For lower and higher pH and pKa (3-11) buffer needs to be more concentrated (at least 0.1 M) for the assumption to yield correct results. Outside of those values (both for higher and lower concentrations and higher and lower pKa values) calculations get complicated, see the discussion on the Henderson-Hasselbalch equation page.
Note, that for now we are ignoring effects of the ionic strength on the solution pH - we will get back to it later.
Let's try another example problems:
How much NaOH must be added to 50 mL of 0.1 M acetic acid to prepare pH 5.0 buffer?
Plugging given pH and known pKa into the Henderson-Hasselbalch equation we get
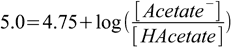 2.3
2.3and after simple rearranging
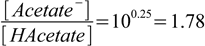 2.4
2.4Now it is just a matter of stoichiometry - added NaOH neutralizes acid and produces acetate ion. Initially there was 0.05 L×0.1 M=0.005 moles of acetic acid, after adding n moles of NaOH there will be 0.005-n moles of acetic acid and n moles of acetate (this is pretty easy, as they react 1:1, we also assume NaOH is a limiting reagent). If so, concentrations of HAcetate and Acetate- are
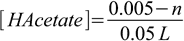 2.5
2.5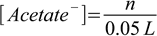 2.6
2.6(we assume volume didn't change) and ratio of concentrations is
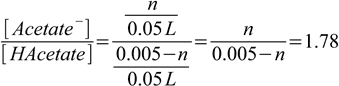 2.7
2.7This equation can be easily solved for n, which is 0.00320 moles - and that's the final answer to the question.
Note how the volumes canceled out in the equation - this is an important property of the Henderson-Hasselbalch equation, one that often speeds up calculations, as it is enough to calculate number of moles of acid and its conjugate base - there is no need to calculate exact concentrations.
How to prepare pH 7.0 phosphoric buffer using 50 mL of 0.01 M H3PO4 and solid NaOH?
This is almost identical problem, with one important difference - we deal with a triprotic acid. pKa values for phosphoric acid are 2.15, 7.20 and 12.35 respectively, of those the second one is very close to the pH we need, so we will prepare buffer using the H2PO4-/HPO42- equilibrium. Once again we will just plug known numbers into the Henderson-Hasselbalch equation:
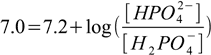 2.8
2.8and calculate ratio of concentrations of the acid H2PO4- and its conjugate base HPO42- by simple rearranging:
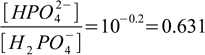 2.9
2.9Now it is a matter of stoichiometry. First, we need to convert all H3PO4 to H2PO4-:
H3PO4 + NaOH → NaH2PO4 + H2O
and, as there are 0.05 L×0.01 M = 5×10-4 moles of H3PO4 we need 5×10-4 moles of NaOH for this step. Then, some of the H2PO4- has to be converted to HPO42-. We already know how to calculate additional amount of NaOH, as calculations now are identical as in the previous question. We have 5×10-4 moles of H2PO4-, and we need n moles of NaOH, where n can be calculated from
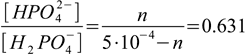 2.10
2.10so n = 1.93×10-4 moles. We already used 5×10-4 moles of NaOH earlier to neutralize first proton of H3PO4, so we need total of 5×10-4+1.93×10-4=6.93×10-4 moles of NaOH.
What volume of 1 M HCl must be added to 100 mL of 0.1 M ammonia to prepare pH 10.0 buffer?
When buffers are prepared from a weak base, calculations can be done in two separate ways. We can use pKa of the conjugate acid, and Henderson-Hasselbalch equation in the pH form, or we can use pKb of the base, and Henderson-Hasselbalch equation in the pOH form. While the latter method yields the same result, we will not test it here, to keep to Brønsted-Lowry theory.
First, we will need pKa of the ammonia. Sometimes it is directly listed in the tables, but quite often what is listed is the pKb value of 4.75. It can be directly plugged into Henderson-Hasselbalch equation in the pKb form, but we will convert it to the pKa of the conjugate acid. Pretty simple, all we need to remember is the relationship
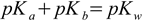 2.11
2.11derived on the water ionic product page. Assuming pKw = 14 we have
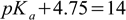 2.12
2.12and pKa = 9.25. Please remember it is pKa of the conjugate acid NH4+, with the dissociation reaction
NH4+ ↔ NH3 + H+
Next steps of the calculations are identical to the ones we have already seen. First, write Henderson-Hasselbalch equation:
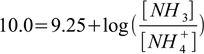 2.13
2.13Second, calculate ratio of the acid and conjugate base:
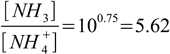 2.14
2.14Third, we started with 0.1L×0.1 M = 0.01 moles of ammonia. We need to add n moles of HCl (let's say these n moles are in the volume V of the hydrochloric acid solution, so the final volume of the solution is V+0.05 L, as you will see V cancels out, so we will calculate it later from n), we assume protonation went to completion, so the number of moles of ammonia is 0.01-n, number of moles of NH4+ is n, and their concentrations are:
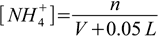 2.15
2.15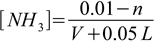 2.16
2.16The concentration ratio is
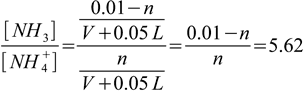 2.17
2.17and n = 0.00151 moles. As we were told to use 1 M solution, required volume is V=n/C=0.00151/1=0.00151 L or 1.51 mL.
How much HCl has to be added to 50 mL of 0.1 M sodium acetate to prepare pH 5.0 buffer?
While it looks as a completely different problem than the previous ones, it in fact doesn't differ at all from the question with buffer prepared from ammonia. Again, we will use the strong acid to produce a weak acid by protonating its conjugate base, and as usual, we will assume reaction went to completion:
NaAcetate + HCl → HAcetate + NaCl
Calculations are identical. First, we need to find the ratio between the acid and the conjugate base:
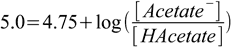 2.18
2.18or (as we have already calculated in an earlier example):
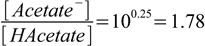 2.19
2.19Concentrations of the HAcetate and Acetate- in the solution after adding n moles of HCl in V L of the HCl solution are:
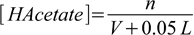 2.20
2.20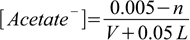 2.21
2.21(where 0.005 mole is the initial amount of acetate present), and the ratio is
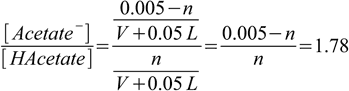 2.22
2.22Now we can calculate n (required amount of HCl) to be 0.00180 moles. Not surprisingly, if you take a look at the earlier question (pH 5.0 buffer from acetic acid and NaOH) number of moles of NaOH calculated there was 0.00320, and 0.00320+0.00180 = 0.005 - which is a total number of moles of acetic acid and acetate present in both solutions.
How to prepare 200 mL of pH=4.5 0.1 M acetate buffer from 2 M acetic acid and 1 M sodium acetate?
As usual, we know ratio of concentrations from the Henderson-Hasselbalch equation:
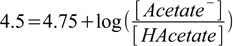 2.23
2.23or:
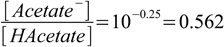 2.24
2.24This question requires an additional step, as there is an additional constraint put on the buffer concentration. 0.1 M acetic buffer means that sum of concentrations of acetic acid and acetate is 0.1 M:
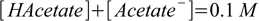 2.25
2.25Now we have two equations in two unknowns, so we can solve them. This is a pretty simple algebra, yielding:
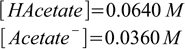 2.26
2.26Sometimes this would be a final answer, in this case we need to do some additional dilution calculations. We need 0.2 L of the solution, it will contain 0.2 L×0.0640 M = 0.0128 moles of acetic acid, so we need 0.0128 moles/2 M = 0.0064 L (or 6.4 mL) of the 2 M acetic acid solution. We also need 0.2 L×0.0360 M = 0.00720 moles of sodium acetate, or 0.00720 moles/1 M = 0.0072 L (or 7.2 mL) of the 1 M sodium acetate solution. The final recipe is 6.4 mL of 2 M acetic acid, plus 7.2 mL of 1 M sodium acetate, filled up to 200 mL.
Note that in some earlier questions final concentration of the buffer was also controlled by the way it were prepared (almost no change in volume when adding solid NaOH, or mixing 0.1 M solutions of both acetic acid and sodium acetate). These are all valid methods of preparing the buffer of known concentration.



